I haven’t posted in quite a while, and I feel pretty bad for not finishing the lattice posts yet (I’m working on them I promise) so here’s a short filler post about Glasser’s master theorem. I find it quite interesting, and the Wikipedia page doesn’t really contain much, so hopefully this will be useful.

the theorem#

For \(a, a_1, a_2, \dots, a_n, b_1, b_2, \dots, b_n \in \mathbb{R}\) and \(a_1, a_2, \dots, a_n > 0\), we have that

\[ \int_{-\infty}^\infty f\left(x+a-\sum_{i=1}^{n}\frac{a_i}{x-b_i}\right) dx = \int_{-\infty}^\infty f\left(x\right) dx \]

Now let’s see an example of an integral that can be easily solved with this theorem.

Find \(\int_{-\infty}^\infty \frac{x^2}{x^4+x^2+1} dx\).

A conventional method with partial fraction decomposition would be pretty unwieldy:

\[ \begin{align} \int_{-\infty}^\infty \frac{x^2}{x^4+x^2+1} dx &= \int_{-\infty}^\infty \frac{x^2}{x^4+2x^2+1 - x^2} dx\\ &= \int_{-\infty}^\infty \frac{x^2}{\left(x^2+x+1\right)\left(x^2-x+1\right)} dx\\ &= \frac{1}{2} \int_{-\infty}^\infty \left( \frac{x}{x^2-x+1} - \frac{x}{x^2+x+1} \right) dx\\ &= \frac{1}{4} \int_{-\infty}^\infty \left( \frac{2x-1}{x^2-x+1} + \frac{1}{x^2-x+1} - \frac{2x+1}{x^2+x+1} + \frac{1}{x^2+x+1} \right) dx\\ &= \left.\frac{1}{4} \ln \left( \frac{x^2-x+1}{x^2+x+1} \right) \right\vert_{-\infty}^\infty + \frac{1}{4} \int_{-\infty}^\infty \left( \frac{1}{x^2+x+1} + \frac{1}{x^2-x+1} \right) dx\\ &= \frac{1}{4} \left( \int_{-\infty}^\infty \frac{1}{x^2-x+1} dx + \int_{-\infty}^\infty \frac{1}{x^2+x+1} dx \right)\\ &= \frac{1}{4} \left( \int_{-\infty}^\infty \frac{1}{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}} dx + \int_{-\infty}^\infty \frac{1}{\left(x+\frac{1}{2}\right)^2+\frac{3}{4}} dx \right)\\ &= \frac{1}{4} \left( \int_{-\infty}^\infty \frac{1}{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}} dx + \int_{-\infty}^\infty \frac{1}{\left(x+\frac{1}{2}\right)^2+\frac{3}{4}} dx \right)\\ &= \left. \frac{1}{2\sqrt3} \left( \arctan\left(\frac{2x-1}{\sqrt3}\right) + \arctan\left(\frac{2x+1}{\sqrt3}\right) \right) \right\vert_{-\infty}^\infty\\ &= \frac{1}{2\sqrt3} \left( \pi + \pi \right)\\ &= \frac{\pi}{\sqrt3} \end{align} \]

It’s very simple to make mistakes like sign errors in long workings like this.¹ But using Glasser’s master theorem,

\[ \begin{align} \int_{-\infty}^\infty \frac{x^2}{x^4+x^2+1} dx &= \int_{-\infty}^\infty \frac{1}{x^2+x^{-2}+1} dx\\ &= \int_{-\infty}^\infty \frac{1}{(x-x^{-1})^2+3} dx\\ &= \int_{-\infty}^\infty \frac{1}{x^2+3} dx\\ &= \left. \frac{1}{\sqrt3} \arctan\left(\frac{x}{\sqrt3}\right) \right\vert_{-\infty}^{\infty}\\ &= \frac{\pi}{\sqrt3} \end{align} \]

This looks much neater² than the first solution.

the proof#

From here onwards, we will assume that \(b_1 < b_2 < \dots < b_n\). Let’s take a look at what the substitution looks like. As a reminder, the theorem states that

\[ \int_{-\infty}^\infty f\left(u\left(x\right)\right) dx = \int_{-\infty}^\infty f\left(x\right) dx \]

where \(u(x)=x+a-\sum_{i=1}^{n}\frac{a_i}{x-b_i}\).

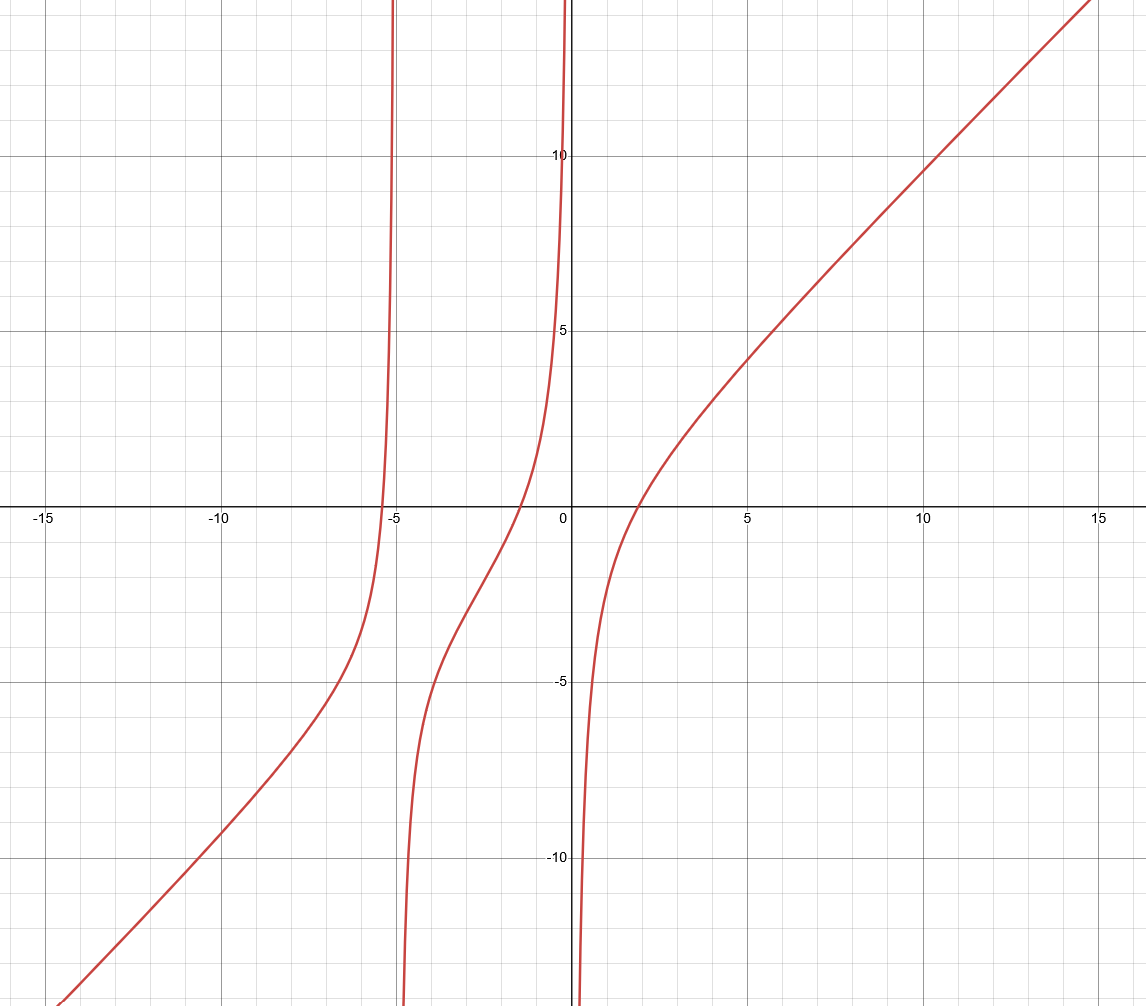
In general, the graph is made up of \(n+1\) continuous “pieces”, with discontinuities between the pieces at \(x = b_i\). We can denote these pieces as \(u_0, u_1, \dots, u_n\), which are continuous on \(\left(-\infty, b_1\right), \left(b_1, b_2\right), \left(b_2, b_3\right), \dots, \left(b_n, \infty\right)\) respectively. It’s easy to see that the inverses of these pieces, \(u_i^{-1}\), all satisfy the equation \(u\left(u_i^{-1}\left(x\right)\right)\). We will denote the inverses as \(u_i^{-1} = v_i\).

Now, we consider the equation \(u\left(x\right) = 0\) and multiply to get rid of the denominators in the expression of \(u\left(x\right)\) and obtain a polynomial in \(x\)³:

\[ \begin{align} \left(x+a\right) \prod_{i=1}^n \left(x-b_i\right) - \sum_{i=1}^n a_i \prod_{i=1}^n \left(x-b_i\right) &= \left(x+a\right)\left(x-b_1\right)\left(x-b_2\right)\dots\left(x-b_n\right)\\ &- a_1 \left(x-b_2\right)\left(x-b_3\right)\dots\left(x-b_n\right)\\ &- a_2 \left(x-b_1\right)\left(x-b_3\right)\dots\left(x-b_n\right)\\ &\vdots\\ &- a_n \left(x-b_1\right)\left(x-b_2\right)\dots\left(x-b_{n-1}\right) \end{align} \]

Expanding out the products, we get

\[ x^{n+1} + \left(a-b_1-b_2-\dots-b_n\right) x^n + O\left(x^{n-1}\right) \]

Since this is a polynomial with degree \(n+1\), there are at most \(n+1\) solutions, which are exactly \(v_0, \dots, v_n\). From Vieta’s formulas, we also know that \(\sum_{i=0}^n v_i\left(x\right) = -a + \sum_{i=1}^n b_i\).

Now we are ready to put everything together. We can split the original integral into pieces as follows:

\[ \begin{align} &\int_{-\infty}^\infty f\left(u\left(x\right)\right) dx\\ = &\int_{-\infty}^{b_1} f\left(u_0\left(x\right)\right) dx + \int_{b_1}^{b_2} f\left(u_1\left(x\right)\right) dx + \dots + \int_{b_n}^\infty f\left(u_n\left(x\right)\right) dx \end{align} \]

and we then make the substitution \(x = v_i\left(t\right)\) for each integral to get

\[ \begin{align} &\int_{-\infty}^{\infty} f\left(t\right) v_0^\prime\left(t\right) dt + \int_{-\infty}^{\infty} f\left(t\right) v_1^\prime\left(t\right) dt + \dots + \int_{-\infty}^{\infty} f\left(t\right) v_n^\prime\left(t\right) dt\\ &= \int_{-\infty}^{\infty} f\left(t\right) \sum_{i=0}^{n} v_i^\prime\left(t\right) dt \end{align} \]

But how do we know what \(\sum_{i=0}^{n} v_i^\prime\left(t\right)\) is? We can take the previously obtained expression for \(\sum_{i=0}^n v_i\left(x\right)\) and differentiate with respect to \(x\) to get

\[ \sum_{i=0}^n v_i^\prime\left(x\right) = 1 \]

and so

\[ \int_{-\infty}^\infty f\left(u\left(x\right)\right) dx = \int_{-\infty}^\infty f\left(x\right) dx \]

Hence proven.